Slump method B
. 
Blue ob
. 
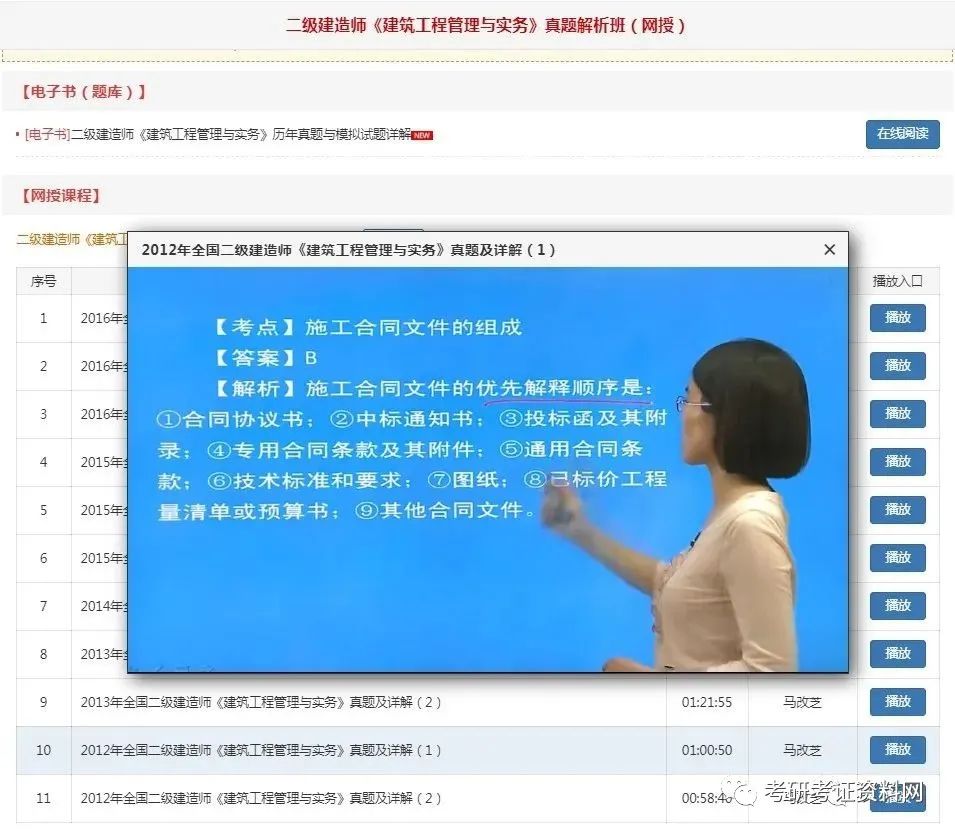
pouring cushion construction engineering laws and regulations examination question [answer] d construction engineering laws and regulations examination question [analysis] when the cantilever support structure displacement, should take add support or anchor, support wall back unloading and other methods to deal with in time
. 
The temperature of concrete pouring into the mold shall not be higher than 35 ℃
. 
OA
. 
The greater the consistency value is, the smaller the fluidity is
. 
construction engineering regulations examination question [analysis] reliability assessment of existing structures can be divided into safety assessment In addition, it is necessary to evaluate the ability to resist disasters
. 
When deep sliding occurs in cantilever foundation pit supporting structure, the measures that should be taken in time are as follows
. 
For the dry and hard concrete mixture with slump value less than 10 mm, the consistency measured by Weibull consistency test is used as the fluidity index
. 
A
. 
H), measures should be taken to prevent wind, sunshade and spray on the construction surface
. 
A
. 
The corrosion mechanism of steel bar and concrete in chemical corrosion environment is ()
. 
The connection between infilled wall and frame can be separated or not separated according to the design requirements
. 
corrosion of concrete caused by sulfate and other chemicals Please
. 
Concrete pouring should be carried out in the morning or at night, and should be continuous
. 
flow velocity method construction engineering regulations examination question [answer] a construction engineering regulations examination question [analysis] slump test is commonly used on construction site to determine the slump or slump expansion of concrete mixture
. 
concrete damage caused by repeated freeze-thaw C
.
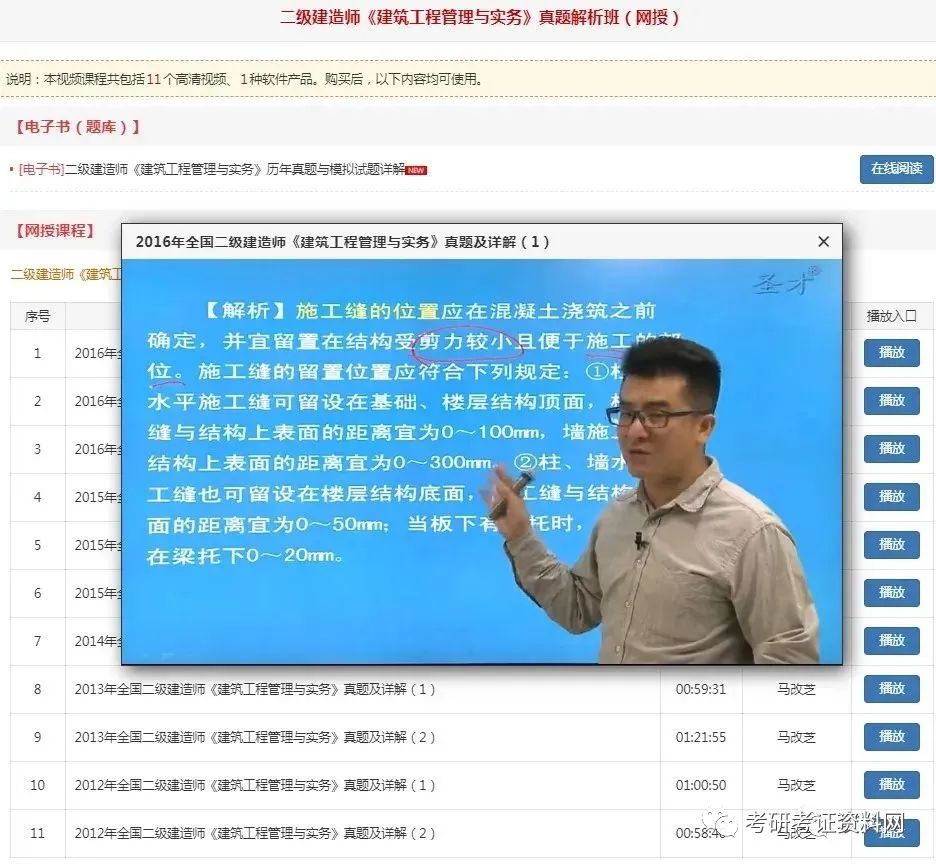
When the height of the wall exceeds 6 m, the horizontal tie beam connecting with the column should be set every 2 m along the wall height, and the section height of the tie beam should not be less than 60 mm
.
durability assessment D
.
Before the removal of the side formwork, the wet curing with formwork should be adopted
.
According to the code for durability design of concrete structures (GB / t50476-2008), the environment of the structure can be divided into the following five categories according to the corrosion mechanism of reinforcement and concrete materials, as shown in Table 1
.
After the completion of concrete pouring, the moisture conservation shall be carried out in time
.
Weibull consistency method D
.
Before concrete pouring, sunshade measures should be taken on the construction working surface, and water spraying and other cooling measures should be taken on the formwork, reinforcement and construction equipment, but there should be no ponding in the formwork during pouring
.
Gray OD
.
A
.
support wall back unloading D
.
safety assessment B
.
The cohesiveness and water retention of concrete mixture are mainly evaluated by visual inspection combined with experience
.
Test question 6: the fluidity of concrete mixture is often measured on construction site
.
corrosion of reinforcement caused by carbonation of concrete cover D
.
Among them, the safety evaluation should include three evaluation items: structural system and component layout, connection and structure, and bearing capacity; the applicability evaluation refers to that under the condition that the structural safety is guaranteed, the applicability problems such as deformation, crack, displacement and vibration that affect the normal use of the structure should be evaluated according to the requirements of the current structural design standards; and the durability evaluation should be based on the requirements of the current structural design standards For the purpose of judging the relationship between the corresponding durability life and the evaluation service life of the structure, the comprehensive evaluation should be carried out from the aspects of structural system and component layout, connection and structure, bearing capacity, disaster prevention and mitigation and protective measures
.
disaster resistance assessment examination question of building engineering regulations [answer] B
.
When the evaporation rate of water is greater than 1kg/ (m2
.
Examination question 2 of building engineering regulations: the assessment of cracks affecting the normal use of structural members of existing buildings belongs to error correction in reliability assessment
.
A
.
When there are seismic fortification requirements, the method of () should be used between infilled wall and frame
.
As a liquidity index, the greater the slump or slump expansion, the greater the fluidity
.
Corrosion of reinforcement caused by chloride salt B
.
In case of deep sliding of cantilever support structure, the cushion should be poured in time, and the cushion can be thickened if necessary to form the lower horizontal support
.
A complete set of examination questions of construction engineering laws and regulations! During the hot weather, the color of the tank body of the concrete mixer truck is () usually
.
When the infilled wall is separated from the frame, when the height of the wall is more than 4m, the horizontal tie beam connected with the column should be set in the middle and middle part of the wall, the section height of the tie beam should not be less than 60mm, and the height of the infilled wall should not be more than 6m; when the infilled wall is not separated from the frame, when the length of the infilled wall is more than 5m or the length of the wall is more than twice the height of the floor, the wall top and the beam should be connected, and the middle part of the wall should be provided with a structure When the height of the wall exceeds 4 m, the horizontal tie beam connecting with the column should be set in the middle and middle part of the wall
.
When there are seismic fortification requirements, the method of separating the infilled wall from the frame should be adopted
.
penetration method C
.
A
.
add support C
.
Green OC
.
Applicability Assessment C
.
Copyright notice: This article is excerpted from the key learning network! Copyright content is prohibited without permission
.
White building engineering regulations examination question [answer] D building engineering regulations examination question [examination point] construction technology in high temperature weather; building engineering regulations examination question [analysis] concrete should be transported by concrete mixer truck with white coating; concrete conveying pipe should be covered with sunshade and watered to reduce temperature
.
Add anchor B
.